文科省リーディングプロジェクト
「革新的イノベーション創出プログラム（COI STREAM）」
2人の東大医科研教員陣＋8人の生命系博士号を持った専門家チーム

文部科学省と独立行政法人科学技術振興機構の「革新的イノベーション創出プログラム（COI STREAM）」における東京大学医科学研究所とDeNAライフサイエンスの共同研究として、遺伝子情報をさまざまな疾病のリスク予測、体質の解析に利用できるロジックを作成するチームを結成しました。生命系のPh.Dを持つ専任研究員8名と東大医科学研究所の教員陣2名の総勢10名体制で、世界の先端研究を分析しています。
このチームが研究論文の分析を行い、毎週の定例ミーティングを通じ、最終的に予測に用いる科学的根拠を選定しました。

信頼性の高い研究の採用
～MYCODEにおける遺伝子検査ロジックの構築～

1. 論文の選定

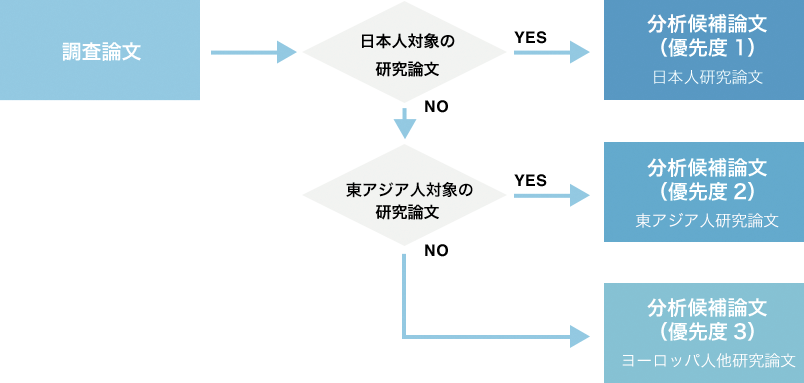
下記のフローで優先度付けがなされた論文のうち、疾患については最高優先度の論文を全て、体質については最高優先度論文から研究の規模・質に基づき最適な論文を一報選定し、それぞれ分析へと進みます。

2. SNPの選定

分析の対象となった論文は、専任の研究員により分析され、必要な情報がデータベース化されます。
構築されたデータベースの中から、統計的に有意（P値と呼ばれる“確からしさ”の指標が5.0×10のマイナス8乗未満）とみなされた複数のSNPで、かつそれぞれ遺伝的に独立な（連鎖していない）SNPの組み合わせをリスクモデルに適用します。連鎖していないかどうかは、各SNPがそれぞれ5Mb以上離れているかを確認しています。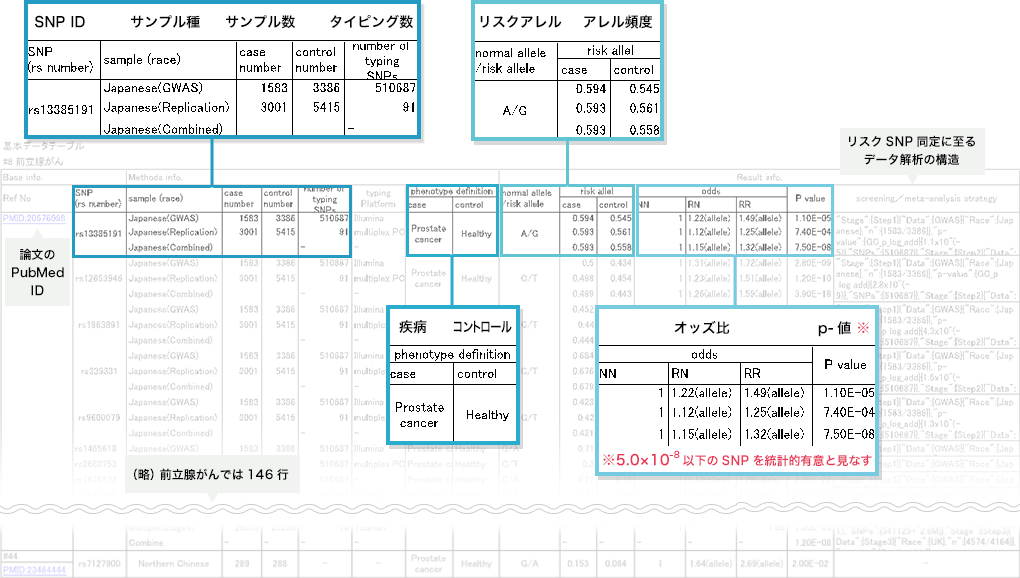

3. リスクモデルの構築

ある病気についてあるSNPが関連していると言うことがGWASを用いた研究により分かり、そのSNPのリスクアレル（Rと書きます）とノンリスクアレル（Nと書きます）の情報がその研究により得られます。具体的には、

• ●ノンリスクホモ（NN）に対するリスクヘテロ（RN）のオッズ比
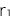
• ●ノンリスクホモ（NN）に対するリスクホモ（RR）のオッズ比

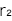
です。この２つの値は、GWASにおける症例（ケース）と対照（コントロール）における各遺伝型の標本数をまとめた次の表

	NN	RN	RR
対照	A	B	C
症例	D	E	F

を用いて

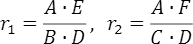
で得られます。ここでは、この情報を使ってどのように発症確率を計算しているかを説明します。

今、リスクアレルの頻度を p とすると、ノンリスクアレルの頻度は 1 ― p となり、ハーディ・ワインベルグ平衡の下では、３つの遺伝型NN、RN、RRの頻度は

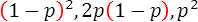
となり、NN、RN、RRの浸透率（penetrance）を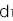,,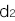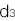と表すと、この病気の発症確率 q は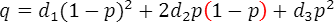

となります。ここで、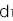,,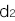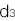はそれぞれNN、RN、RRの集団におけるこの病気の発症確率となります。この病気の集団全体での発症確率qが分かっているとします。すると、これら３つの確率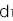,,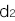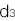は、GWASより求めたオッズ比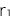,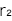を用いて求めることができます。その方法の概略を示します。
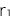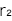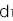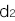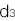オッズ比,は,,を用いて、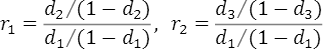

と表すことができます。この２つの式をそれぞれ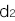,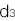について解き、上の発症確率 q の式に代入します。すると、２つのオッズ比が１でなければ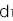の３次方程式を得ますので、それを解くことによって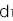を得ることができます。この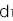から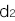,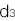が上のオッズ比の２つの式から得られますので、これで３つの遺伝型の発症確率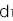,,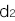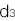を求めることができました。

今、複数のSNPがこの病気と関係しているとすると、各SNPについて上の方法により浸透率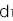,,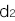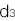を求めることができます。ここでは n 個のSNPがこの病気に関係しているとします。i番目のSNPの浸透率を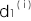,,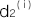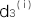と書くことにします。ある遺伝型の集団（上記のn個のSNPのパターンが同じ集団）を考えます。その集団のi番目のSNPの遺伝型に対する浸透率を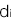と書きます。ただし、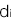は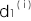,,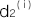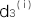のどれかとなります。このとき、この病気の集団全体の発症確率 q に対するこの集団の発症確率 P のリスク比が次の乗法モデルで計算されると仮定します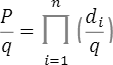

この関係式を使い、この集団の発症確率Pは

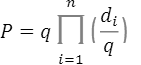
と計算されます。
補足となりますが、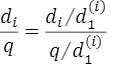

ですので、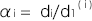,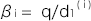とおくと、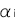は、この集団のノンリスクホモ（NN）に対する発症のリスク比、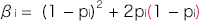∙∙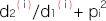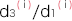は、このSNPの発症リスク比の平均となり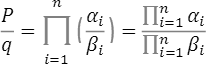

の分母はこの疾患の平均発症リスク比、分子はn個のSNPに基づくこの集団のリスク比を表しています。ただし、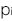はi番目のSNP におけるリスクアレル頻度です。

4. 論文評価レベルの基準

『MYCODEの遺伝子検査では、統計的な確からしさが十分である事が確認されたSNP（P値が5.0×10のマイナス8乗未満）のみを採用しています。各項目は参照した研究の情報をもとに、論文評価レベルとして3段階に定義しています。』

• ●下記1～3の点数を足し合わせ、下記の定義で最終的な星の数を決める。
  （なお、SNPが複数ある項目は合計点数の平均値をとる(小数点以下切捨て)
• ●合計点数が、12～18：/ 9～11：/ 6～8：

• 1.人種カテゴリー

  • 日本人：9点
  • 東アジア（日本人以外）：6点
  • ヨーロッパ他：3点
  • 寄与度が最も高く、重要な指標と考えられるので3点間隔で定義

• 2.サンプルサイズ

  【疾患】

  • ケース数 ≧ 1000 かつ
    コントロール数 ≧ 1000：
    3点
  • ケース数 ≧ 1000 または
    コントロール数 ≧ 1000：
    2点
  • ケース数 < 1000 かつ
    コントロール数 < 1000：
    1点

  【体質】

  • サンプルサイズ ≧ 8000：3点
  • 8000 > サンプルサイズ ≧ 4000：2点
  • サンプルサイズ < 4000：1点
  • p-値ですでに考慮されていることになるので1点間隔で定義

• 3.再現性(別集団でも再現できているか)

  • 別論文として報告あり：6点
  • 同一論文内で
    別データの検証報告あり：
    4点
  • 全くなし：2点
  • 人種・サンプルサイズに比べ影響が中程度となるので2点間隔で定義